The Linear Algebra behind Wall Jumping
Linear Algebra plays a huge role in game development, especially within movement and projectile systems.
In my parkour demo, I make use of key Linear Algebra concepts, the Cross Product and Dot Product, to tailor the wall jumping functionality to my needs.
Calculating Jump Direction using the Cross Product
In the demo, the player clings to wall-jumpable walls when they jump onto it. From this point, they can jump off of this wall based on the direction they are facing relative to the wall.
To achieve this functionality, we only need a couple vectors:
- Wall Normal Vector (the normal relative to the plane of the wall we are clinging to)
- Camera Forward Vector (the current direction the camera is facing)
Since we’re only worried about the angle relative to the Wall Normal, we ignore the vertical-axis (Z-axis in Unreal) of these two vectors.
We get the cross product of the Camera Forward Vector and the Wall Normal Vector (order matters in cross product!!!).
Cross Product
Here are a few key things to know about the cross product:
-
The cross product of two vectors results in a vector that is perpendicular to both vectors
-
Since it gives a perpendicular vector, it can be used to find the normal vector of a plane (Not relevant here, but good to know)
-
The equation for the cross product is: $a \times b = (a_yb_z - a_zb_y, a_zb_x - a_xb_z, a_xb_y - a_yb_x)$
-
Since our Camera and Wall vectors have no Z-value, the x and y values of the new vector will be 0.
Calculation
We then take a look at the Z-component of the resulting Cross Product, which is equivalent to $C_x W_y - C_y W_x$.
Since Unreal uses a left-handed coordinate system, we can determine the following:
- If the resulting vector is positive, we rotate clockwise along the Z-axis, also known as a positive yaw.
- If the resulting vector is negative, we rotate counter-clockwise along the Z-axis, also known as a negative yaw.
- With a right-handed coordinate system, positive would be counter-clockwise, and negative would be clockwise.

The reason the polarity of the Z-component is directly equivalent to the polarity of the yaw is because yaw itself is defined as a rotation about the Z-axis.
Our cross product’s Z-component calculation, $C_x W_y - C_y W_x$, also shows this, as it gives us the relative orientation of the vectors.
When it is positive, the angle formed between the two vectors is a result of $C$ being rotated counter-clockwise relative to $W$, and naturally clockwise relative to $W$ when it is negative.
With this, we can apply a set rotation value, allowing us to always jump in the direction we’re facing!
Implementation
FRotator CameraRotation = GetController()->GetControlRotation();
// Get the forward vector of the camera
FVector CameraForward = CameraRotation.Vector();
FVector WallNormal = WallHit.ImpactNormal;
WallNormal.Z = 0.f;
CameraForward.Z = 0.f;
// Calculate the cross product to determine the side of the wall the camera is facing
FVector CrossProduct = FVector::CrossProduct(CameraForward, WallNormal);
// Check Z component of cross product to see if its left or right
float YawDirectionMultiplier = (CrossProduct.Z > 0.f) ? 1.f : -1.f;
//Apply yaw-rotation so character jumps away from wall
FRotator Rotation = FRotator(GetActorRotation().Pitch, GetActorRotation().Yaw + (120.f * YawDirectionMultiplier), GetActorRotation().Roll);
// Store the desired rotation target for smooth interpolation
FRotator TargetRotation = FRotator(CameraRotation.Pitch, WallNormal.Rotation().Yaw - (50.f * YawDirectionMultiplier), CameraRotation.Roll);
// Rotate player in direction of jump
SetActorRotation(Rotation);
Jumping Towards the Ground with Dot Product
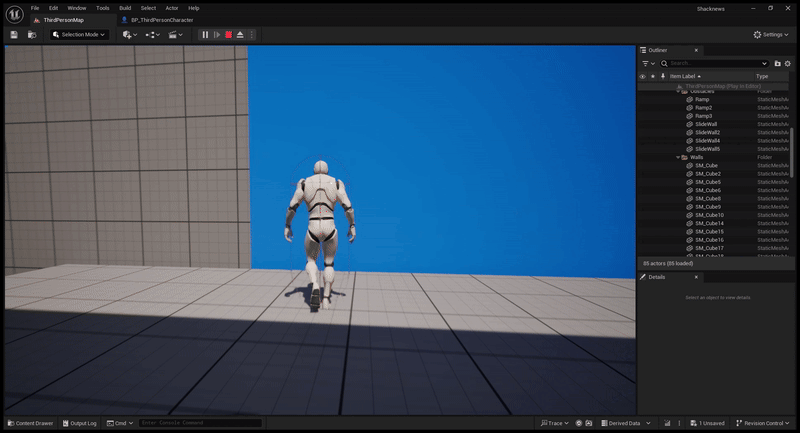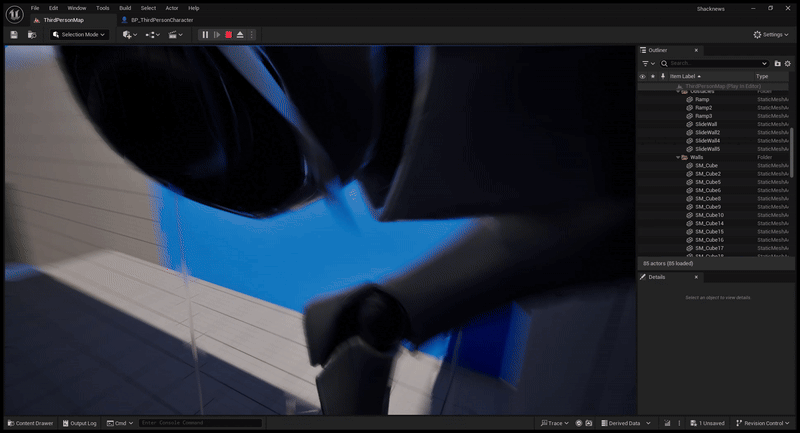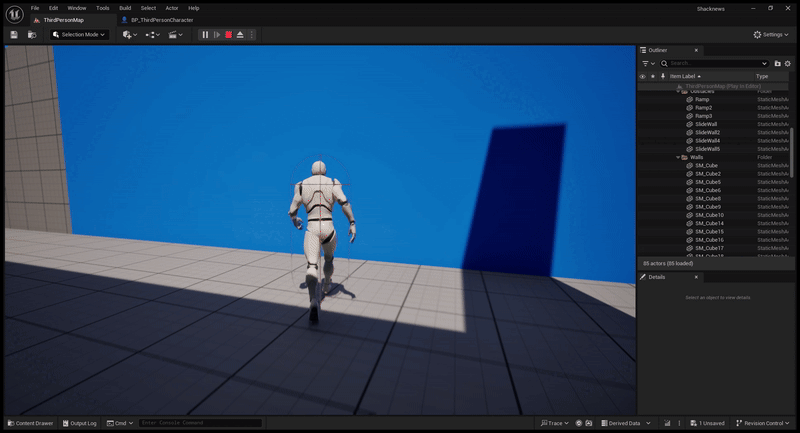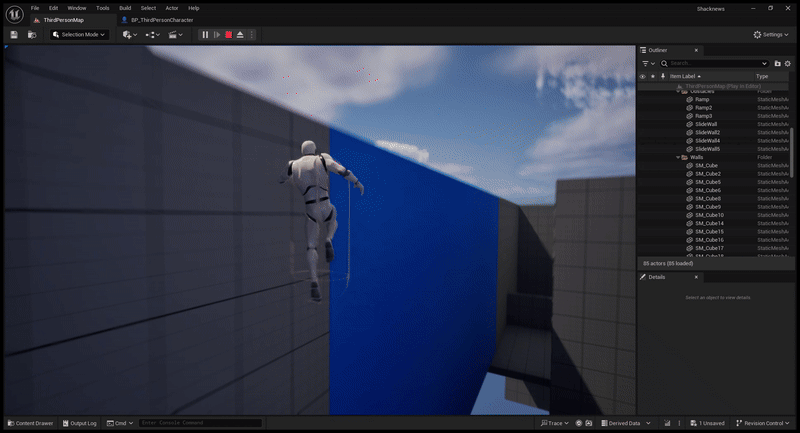
The demo also allows players to choose between a standard wall jump and a wall jump aimed towards the ground.
The player can do this ground jump by looking towards the ground when jumping off a wall.
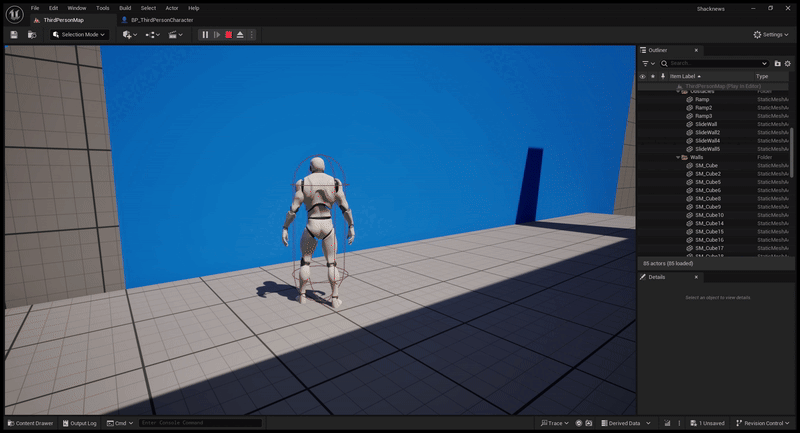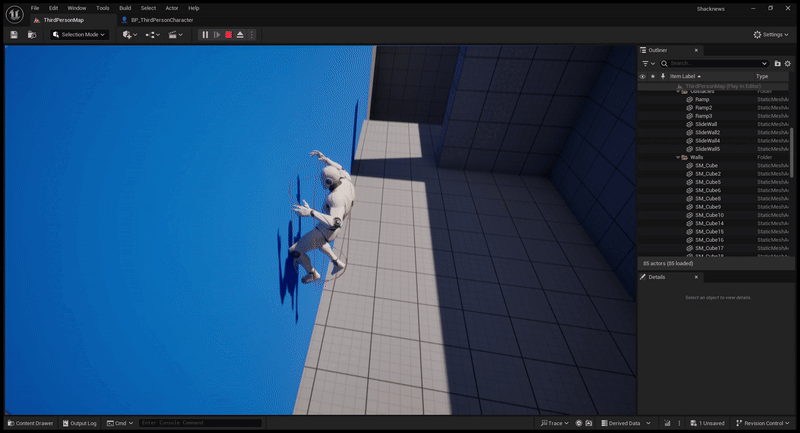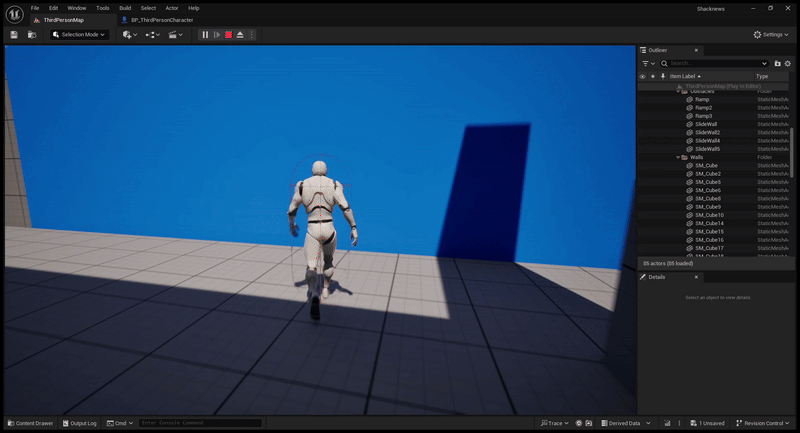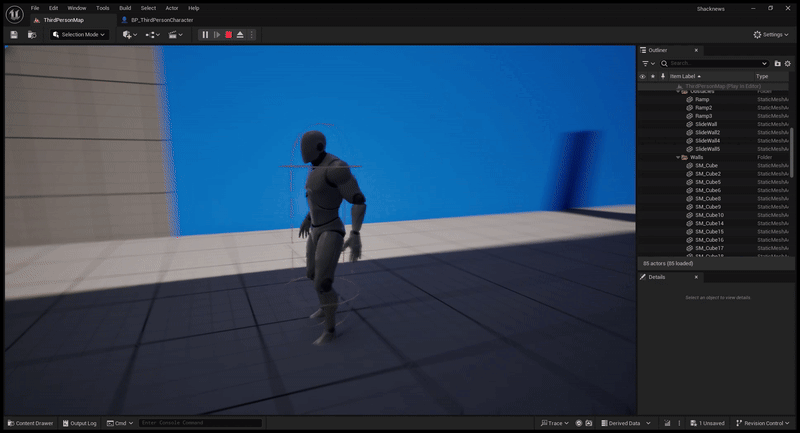
To get this working, all we need is the Player Camera’s Global Rotation vector. This happens to be a unit vector, which makes calculations easier for us.
We calculate the dot product of this rotation vector and the downwards unit vector, resulting in a scalar value that tells us how orthogonal the camera is to the ground.
Dot Product
Here are a few key things to understand about the dot product:
-
Vectors are fully orthogonal when they are perfectly perpendicular, forming right angles.
-
The closer to 0 the resulting value, the more orthogonal the two vectors are, and vice versa. The dot product of orthogonal vectors is 0.
-
The equation for the dot product is $a \cdot b = a_xb_x + a_yb_y + a_zb_z$.
-
The dot product is equivalent to $\text{cos } \theta$, where $\theta$ is the angle formed by the two vectors.
-
The dot product of vectors forming acute angles is positive, while the dot product of values forming obtuse angles is negative.
Calculation
Because of this, we are certain that for dot product values above 0, we are facing downwards, and for values less than 0, we are facing upwards.
To add some bias towards an upwards jump, we set our minimum value for downwards jumping to a dot product of 0.5, where 1 is completely down and -1 is completely up.
We know this because our vectors are unit vectors (vectors with a length of 1) so the maximum possible dot product is 1.
This means that our downwards jump only triggers if the camera is 60 degrees from the horizontal.
This is the case because $\text{cos}^{-1}(0.5) = 60 ^{\circ}$, and the dot product is equivalent to $\text{cos } \theta$.
And so we now have an adjustable downwards wall jump!
Implementation
// Calculate how much the camera is looking downward
FVector CameraWorldForward = GetController()->GetControlRotation().Vector();
float DotWithDown = FVector::DotProduct(CameraWorldForward, FVector(0.f, 0.f, -1.f)); // Dot product with downward vector (world Z)
// Launch character away from wall in correct direction
FVector LaunchVelocity = (GetActorForwardVector() * 2000.f);
// If looking downward, launch towards the ground
if (DotWithDown > 0.5f)
{
LaunchVelocity.Z = DownwardsJumpVelocity; // Launch downwards
}
Conclusion
And thats that! Pretty cool what basic linear algebra can achieve, and it’s especially cool seeing how these different operations and values interact in-game.
You might be thinking that the same approach taken for the dot product could be taken with the wall jump direction, and you’d be right!
It works just as well, and might even be more elegant, but the cross product method came to mind first, and the important thing is that it works and isn’t computationally heavy.
I hope this was a fun (or useful) read!
-Asaad.